実ベクトルで理解する複素ベクトルの世界！

複素ベクトルは、数学や物理学の様々な分野で広く用いられている重要な概念です。しかし、実ベクトルとの関係や、複素平面上での幾何学的意味合いについての理解が不足している者も多くいます。本稿では、実ベクトルを基盤として複素ベクトルの世界を具体的に理解することを目指し、複素平面上での幾何学的操作や、実ベクトルの延長としての複素ベクトルの意味合いについて説明します。

実ベクトルで理解する複素ベクトルの世界！

複素ベクトルは、数学的にはimaginary unitとして知られるiを用いて、実ベクトルとimaginaryベクトルの合成から構成される。しかし、実ベクトルの世界で理解する複素ベクトルというのは、数学的な定義に囚われないための新しいアプローチを提供する。具体的には、複素平面上の点を実ベクトルとして捉えることで、複素ベクトルの操作をより視覚的に理解することができる。

複素ベクトルの定義と性質

複素ベクトルは、実ベクトルとimaginaryベクトルの積として定義される。具体的には、複素ベクトルz = x + yiは、実ベクトルxとimaginaryベクトルyiの積として表される。ここで、xは実ベクトル、yはimaginaryベクトル、iはimaginary unitである。

<td'yi

複素ベクトル	実ベクトル	imaginaryベクトル
z = x + yi	x

複素平面上での視覚化

複素ベクトルを実ベクトルとして捉えることで、複素平面上での視覚化が可能になる。複素平面上では、実軸とimaginary軸が交わる地点に、複素ベクトルの端点が存在する。この視覚化により、複素ベクトルの加算や скаляр積の計算をより簡単に行うことができる。

複素ベクトルの操作

複素ベクトルの操作には、加算、スカラー倍、内積などがある。これらの操作は、実ベクトルの操作と類似しているが、imaginary unitの存在により、複素ベクトルの場合には異なる結果が生じる。複素ベクトルの加算では、実部とimaginary部それぞれについて加算を行う。複素ベクトルのスカラー倍では、スカラー値との積を計算する。

実ベクトルでの複素ベクトルの表現

実ベクトルでの複素ベクトルの表現には、複素ベクトルの実部とimaginary部を独立に捉える方法や、複素ベクトルを実ベクトルのpairとして捉える方法などがある。これらの方法により、複素ベクトルの操作をより簡単に行うことができる。

複素ベクトルの応用

複素ベクトルの応用には、電気工学、信号処理、画像処理などがある。これらの分野では、複素ベクトルを用いて、信号や画像の解析や処理を行う。特に、信号処理では、高速フーリエ変換などのアルゴリズムで複素ベクトルを用いて信号を分析している。

複素数ベクトルとは何ですか？

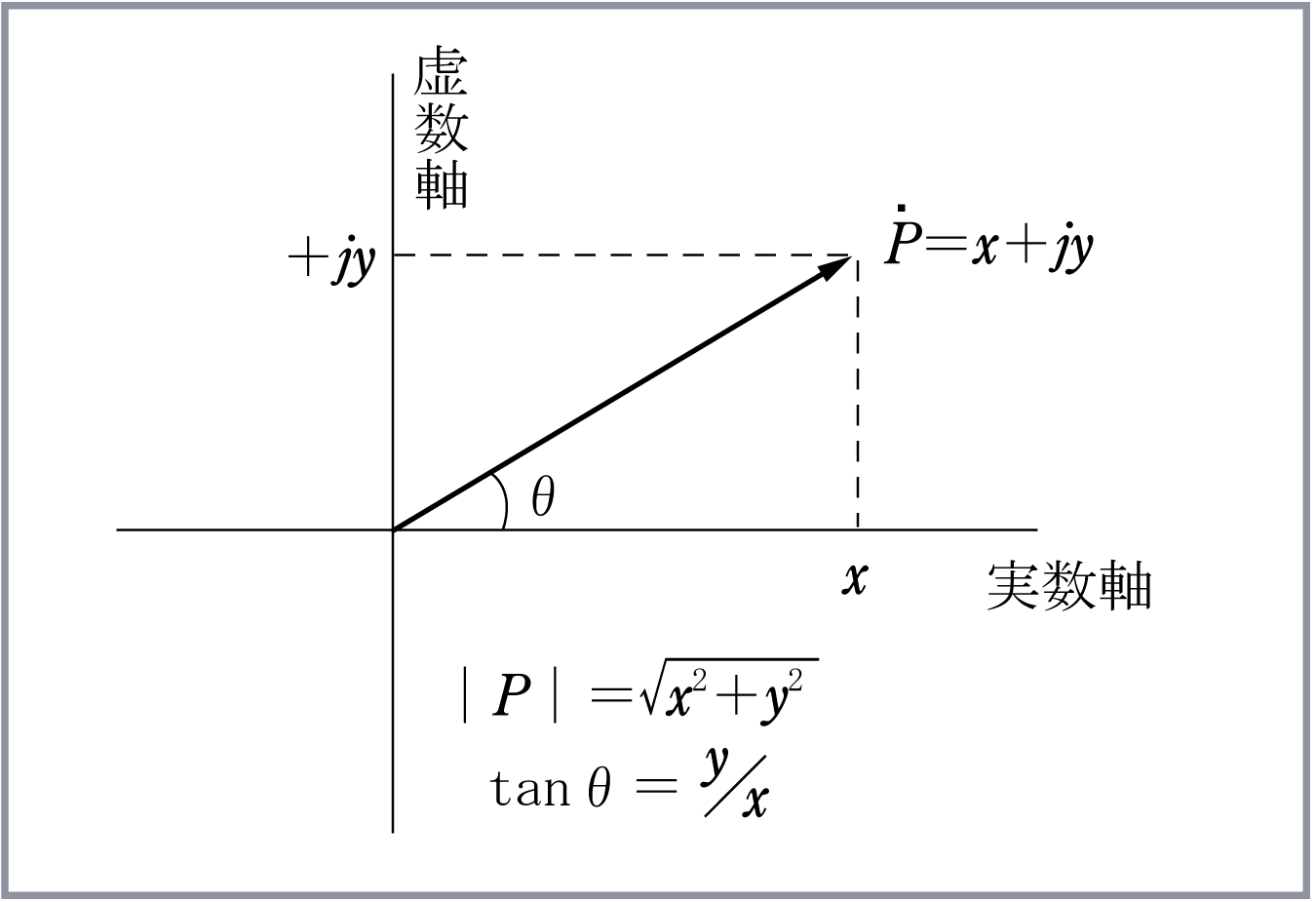
複素数ベクトルは、通常の実数ベクトルと異なり、複素数を成分とするベクトルを指します。複素数ベクトルは、数学や物理学、工学などの分野で幅広く用いられ、特に信号処理や電気工学での応用が著しいです。

複素数ベクトルの定義

複素数ベクトルは、複素数を成分とするベクトル espacio を持つものを指します。複素数ベクトルは、実数ベクトルと同様に演算が可能で、加算や скаляр乗算、内積などが定義されます。

複素数ベクトルの成分は、実部と虚部から構成されます。
複素数ベクトルの演算は、実数ベクトルの演算と同様に行われます。
複素数ベクトルは、oley Hindiスの概念を拡張したものです。

複素数ベクトルの応用

複素数ベクトルは、信号処理や電気工学など、幅広い分野で応用されます。

信号処理では、複素数ベクトルを用いて信号を分析や合成することができます。
電気工学では、複素数ベクトルを用いて交流電流や電圧を表現することができます。
通信工学では、複素数ベクトルを用いて信号伝送の効率化を実現することができます。

複素数ベクトルの特徴

複素数ベクトルは、実数ベクトルと異なり、複素数を成分とするため、以下のような特徴を持ちます。

複素数ベクトルは、複素数の収束を保証することができます。
複素数ベクトルは、 位相の考慮を行うことができます。
複素数ベクトルは、高次元空間での計算を行うことができます。

複素数を考えたのは誰か？

イタリアの数学者カール・フリードリヒ・ガウスが、18世紀末に複素数の概念を初めて導入したと考えられている。ガウスは1799年に出版した著書「Disquisitiones Arithmeticae」において、複素数の数学的性質を調査し、複素数の理論を体系づけた。ガウス以降、複素数の研究は大きく発展し、現在では数学や物理学、工学などの多くの分野で広く応用されている。

複素数の歴史

複素数の概念は、16世紀のイタリアの数学者ジェラルド・カルダーノによって初めて提唱されたと考えられている。カルダーノは、自身の著書「Ars Magna」において、平方根の計算에複素数を用いることを提案した。ただし、カルダーノの提案は当時はあまり受け入れられず、複素数の概念が普及するまでには時間がかかった。

複素数の性質

複素数は、実数と虚数を合わせた数であり、加算や乗算などの四則演算が定義されている。複素数には、絶対値や偏角などの性質があり、これらの性質を利用することで、さまざまな数学的問題を解くことができる。例えば、フーリエ変換やラプラス変換などの数学的技巧では、複素数を用いることで、問題を簡単化することができる。

複素数の応用

複素数は、数学や物理学、工学などの多くの分野で応用されている。例えば、電気工学では、交流電流の計算に複素数を用いることがある。信号処理では、信号の分析や設計に複素数を用いることがある。また、経済学では、複素数を用いて、経済モデルの分析や予測を行うことがある。

電気工学での応用
信号処理での応用
経済学での応用

複素解析とは？

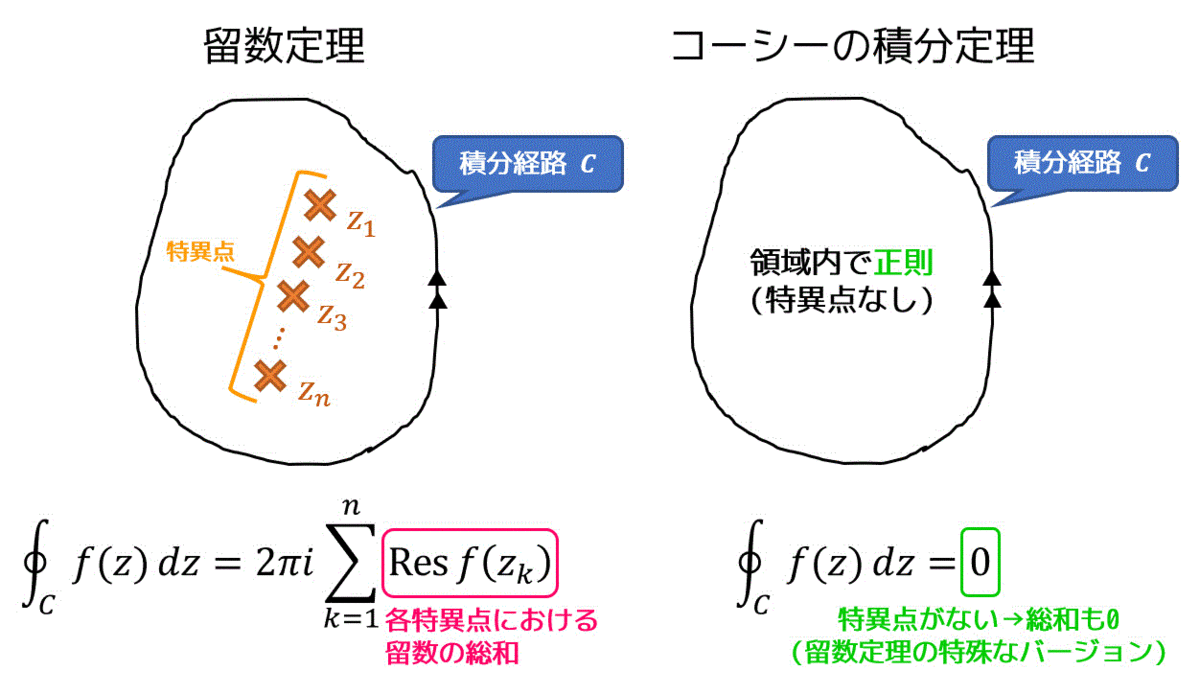
複素解析とは、数学の分野において、複素数平面上での函数の挙動を研究する数学の分野である。複素数は、実数と虚数の和として表される数であり、複素解析では、このような数を扱う函数について研究を行う。

複素解析の歴史

複素解析の歴史は、18世紀初頭に遡る。カール・フリードリヒ・ガウスが、複素数の概念を初めて導入した後、オーギュスタン＝ルイ・コーシー、ベルンハルト・リーマンらが、複素解析の基礎を固める研究を行った。

18世紀：カール・フリードリヒ・ガウスが複素数の概念を導入
19世紀：オーギュスタン＝ルイ・コーシー、ベルンハルト・リーマンらが複素解析の基礎を固める研究を行う
20世紀：複素解析が、函数論、微分方程式論、幾何学などの数学の分野に応用されるようになる

複素解析の重要性

複素解析は、数学の分野において非常に重要な役割を果たしている。特に、函数論、微分方程式論、幾何学などの分野で、複素解析の手法が広く応用されている。

函数論：複素解析は、函数の挙動を研究するために不可欠な手法である
微分方程式論：複素解析は、微分方程式の解を求めるために用いられる
幾何学：複素解析は、幾何学的な問題を解くために用いられる

複素解析の応用

複素解析は、数学の分野以外でも、物理学、工学、情報科学など多くの分野に応用されている。電気工学、電子工学、信号処理などの分野で、複素解析の手法が幅広く用いられている。

電気工学：複素解析は、交流回路の解析や、電力系統の設計に用いられる
電子工学：複素解析は、電子回路の設計や、信号処理に用いられる
信号処理：複素解析は、信号の分析や、画像処理に用いられる

複素数平面は誰が考えましたか？

複素数平面は、カール・フリードリヒ・ガウスによって考案されました。ガウスは、18世紀末期に複素数の理論を体系的に構築し、複素数平面を導入した。ガウスの仕事は、数学の発展に大きな影響を与えました。

複素数平面の歴史

複素数平面は、歴史的に見ると、16世紀にイタリアの数学者ジェロラモ・カルダーノによって初めて導入されました。カルダーノは、解析幾何学の研究を行っていた際に、複素数の概念を提案しました。しかし、当時はまだ複素数の理論が整備されていなかったため、全面的に活用できなかった。後に、18世紀になると、ガウスが複素数の理論を体系的に構築し、複素数平面を導入した。

複素数平面の性質

複素数平面には、以下のような性質があります。

実軸と虚軸に分けることができる。
円を描くことができる。
解析函数を定義することができる。

複素数平面的応用

複素数平面は、数学の各分野に応用されています。

電気工学：交流電圧を表すための複素数が使用される。
機械工学：運動の研究にための複素数が使用される。
情報工学：信号処理にための複素数が使用される。

よくある質問

複素ベクトルとは何ですか？

複素ベクトルは、実数と虚数の両方を含むベクトルを指します。通常、実数は現実世界で観測される値を表し、虚数は純粋イメージの値を表します。複素ベクトルを理解することで、電気工学、機械工学、物理学などの分野で現れる様々な現象を捉えることができます。

実ベクトルと複素ベクトルの違いは何ですか？

実ベクトルと複素ベクトルの最大の違いは、虚数の存在や不存在によるものです。実ベクトルには虚数が含まれませんが、複素ベクトルには虚数が含まれています。このため、複素ベクトルは実ベクトルよりもより広い範囲の値を表すことができます。また、複素ベクトルは相互作用や干渉の計算など、実ベクトルでは捉えないことができる現象を捉えることができます。

複素ベクトルを理解するために必要な数学的知識は何ですか？

複素ベクトルを理解するには、線型代数、微分積分、複素解析などの数学的知識が必要です。特に、複素平面や三角関数の理解は、複素ベクトルの基本的な性質を捉える上で非常に重要です。また、 Fourier 変換やラプラス変換などの数学的ツールをマスターすることも必要です。

複素ベクトルを実際にどのように適用することができますか？

複素ベクトルを実際に適用するには、信号処理、画像処理、 طبیعی言語処理などの分野で様々な応用があります。例えば、音声信号を処理するために複素ベクトルを使用したり、医療イメージングで複素ベクトルを使用して高解像度イメージを生成することができます。また、機械学習や深層学習などの分野でも、複素ベクトルを使用してより良い予測やより良い分类を行うことができます。

Si quieres conocer otros artículos parecidos a 実ベクトルで理解する複素ベクトルの世界！ puedes visitar la categoría Puroguramingu.