難解なガウス過程回帰をわかりやすく解説!
ガウス過程回帰とは、機械学習の分野で広く用いられている統計的モデルですが、その数学的背景や理論的な部分が難解なため、学習するうえで多くの人が苦戦しています。本稿では、ガウス過程回帰の基本的な理論や実際的な応用例をわかりやすく説明し、数学的な背景知識があまりない方でも容易に理解できるようにします。具体的には、ガウス過程の定義や特徴、回帰モデルの構築、ハイパーパラメーターのチューニングなどについて、分かりやすく解説していきます。
難解なガウス過程回帰をわかりやすく解説!
ガウス過程回帰は、机械学習の分野で広く利用されている統計的手法ですが、その理論的な背景や数学的な処理の複雑さ故に、初心者にとっては難解な概念となっています。本記事では、ガウス過程回帰の基礎的な理論やアルゴリズムをわかりやすく解説し、難解な部分を克服するための実践的なTipsを提供します。
ガウス過程回帰の基本概念
ガウス過程回帰の核となるのは、ガウス分布に基づく確率論的な枠組みです。この枠組み속では、観測値と潜在変数の関係を確率的に捉えることができます。ガウス分布は、統計学において最重要の人々の一つで、自然現象の多くがこの分布に従うという特性を持っています。
ガウス過程回帰の数学的な背景
ガウス過程回帰の数学的な背景は、ベイズ統計学の理論に基づいています。ベイズの定理を適用することで、観測値と潜在変数の関係を推論することができます。また、ガウス過程という概念を導入することで、非線形な関係を捉えることができます。
ガウス過程回帰のアルゴリズム
ガウス過程回帰のアルゴリズムには、 expectation-maximization アルゴリズムや variational Bayesian inference アルゴリズムなどがあります。このアルゴリズムを適用することで、ガウス過程回帰モデルの推論を行うことができます。
ガウス過程回帰の実際的な適用
ガウス過程回帰は、機械学習の分野で広く適用されています。時系列予測やスペクトル解析など多くの分野で有効に利用されています。また、推薦システムや自然言語処理の分野でも応用されています。
ガウス過程回帰の難解な部分克服のTips
ガウス過程回帰の難解な部分克服のTipsとして、図解による理論の理解や実際的な問題設定などがあります。また、数学的な背景やアルゴリズムの実装に焦点を当てることで、難解な部分を克服することができます。
| ガウス過程回帰の特徴 | 説明 |
|---|---|
| 確率論的な枠組み | ガウス分布に基づく確率論的な枠組み |
| 非線形な関係捉え | ガウス過程という概念を導入することで、非線形な関係を捉えることができます |
| ベイズ統計学の理論 | ベイズの定理を適用することで、観測値と潜在変数の関係を推論することができます |
| 機械学習の分野での適用 | 機械学習の分野で広く適用されています |
ガウス過程回帰の欠点は何ですか?
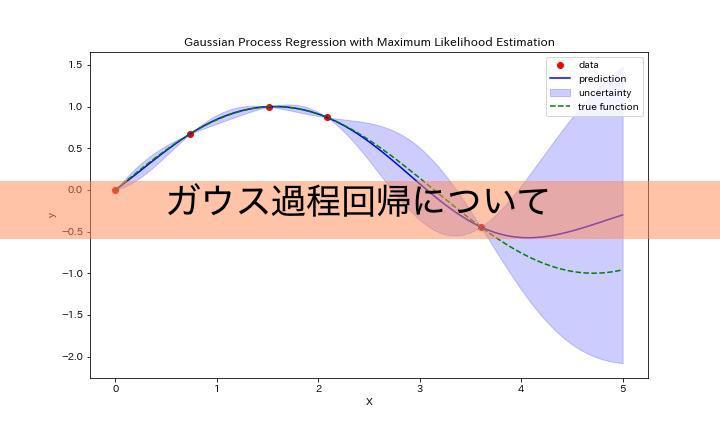
ガウス過程回帰は、機械学習の分野において非常に有効な技術ですが、この技術にもいくつかの欠点があります。
計算コストの高さ
ガウス過程回帰では、ヤコビアン行列の逆行列を計算する必要があります。この計算は非常にコストがかかり、特に大規模なデータセットに対しては計算時間が長くなります。計算コストはガウス過程回帰の主要な欠点の1つです。
- ヤコビアン行列の逆行列の計算には、オーダーを見積もることができます。
- この計算コストは、データセットのサイズや dimensions の数によって影響を受けます。
- 大規模なデータセットでは、高速化するための技術が必要です。
導入の難しさ
ガウス過程回帰は、数学的背景 conocimiento が必要です。数学的(background)が不足している場合、ガウス過程回帰を導入することは困難です。
- ガウス過程回帰は、統計学や機械学習の基礎知識が必要です。
- 特に、ガウス過程の数学的定義や、カーネル関数の選択についての知識が必要です。
- 導入の難しさは、実際の問題に対応するための時間やリソースを要します。
パラメーターの調整の難しさ
ガウス過程回帰では、パラメーター(hyperparameter)を調整する必要があります。パラメーターの調整は、モデル性能の改善に有効ですが、調整の難しさはガウス過程回帰の欠点の1つです。
- パラメーターの調整には、grid searchやrandom searchなどの技術を使用します。
- 調整の難しさは、パラメーターの数や、探索空間のサイズによって影響を受けます。
- 調整の結果、モデル性能の改善には時間やリソースを要します。
ガウス過程とは?

ガウス過程とは、数学において、Brown運動や otras変動を記述するための確率過程の一種です。ガウス分布に従う乱数を用いて、連続的な時間や空間で変動する値を表現します。この過程は、1839年にカール・フリードリヒ・ガウスが導入したため、ガウス過程と呼ばれます。
ガウス過程の特徴
ガウス過程の主要な特徴として、以下のようなものがあります。
- 連続性:ガウス過程は連続的な時間や空間で変動します。
- ガウス分布:ガウス過程はガウス分布に従う乱数を用いて、値を表現します。
- .Markov性:ガウス過程はMarkov性を満たすため、将来の値を予測するために過去の値を考慮する必要がありません。
ガウス過程の応用
ガウス過程は、様々な分野で応用されています。
- finance:金融市場での為替や株価の変動をモデル化するために使用されます。
- signal処理:信号処理において、ノイズ除去やフィルタリングに使用されます。
- 機械学習:機械学習のアルゴリズムにガウス過程を組み込むことで、より高い予測精度を達成することができます。
ガウス過程の種類
ガウス過程には、以下のような種類があります。
- ウィーナー過程:ウィーナー過程は、ガウス過程の特別な場合で、 Brown運動をモデル化するために使用されます。
- オルンシュタイン・ウーレンベック過程:オルンシュタイン・ウーレンベック過程は、ウィーナー過程の拡張版で、多くの物理現象をモデル化するために使用されます。
- Fractional Brownian motion:Fractional Brownian motionは、self-similarityを満たすガウス過程で、ネットワークトラヒックや金融市場での変動をモデル化するために使用されます。
Gausian Processeとはどういう意味ですか?

ガウス過程(Gaussian Process)とは、数学の分野において、確率過程の1種であり、ガウス分布に従うランダム変数を用いてモデリングする手法です。ガウス分布は、平均値と分散を持つ連続的な値を取りうる分布であり、ガウス過程では、この分布に従うランダム変数を時系列や空間的な関係においてモデル化します。
ガウス過程の特徴
ガウス過程の特徴として、以下のような点が挙げられます。
- 非パラメトリック:ガウス過程は、パラメーターの数が有限ではないため、柔軟に対応できるモデルです。
- Bayes的:ガウス過程は、Bayesの定理に基づいて、事前分布と事後分布を計算することができます。
- 計算 tractability:ガウス過程では、計算上のトレードオフを実現できます。
ガウス過程の応用
ガウス過程は、様々な分野において応用されています。
- 機械学習:ガウス過程は、機械学習の分野において、回帰や分类などのタスクにおいて使用されます。
- 信号処理:ガウス過程は、信号処理の分野において、ノイズ除去や信号再構成などのタスクにおいて使用されます。
- ロボット工学:ガウス過程は、ロボット工学の分野において、運動計画や状態推定などのタスクにおいて使用されます。
ガウス過程の数学的背景
ガウス過程の数学的背景として、以下のような点が挙げられます。
- ウィナー・ヒンチン定理:ガウス過程は、ウィナー・ヒンチン定理に基づいて、定義されます。
- カルバック・リー 부등式:ガウス過程では、カルバック・リー 부等式を用いて、誤差を評価します。
- ガウス・マルコフ過程:ガウス過程は、ガウス・マルコフ過程の特別な場合としてримehenいます。
GPとは機械学習で何ですか?
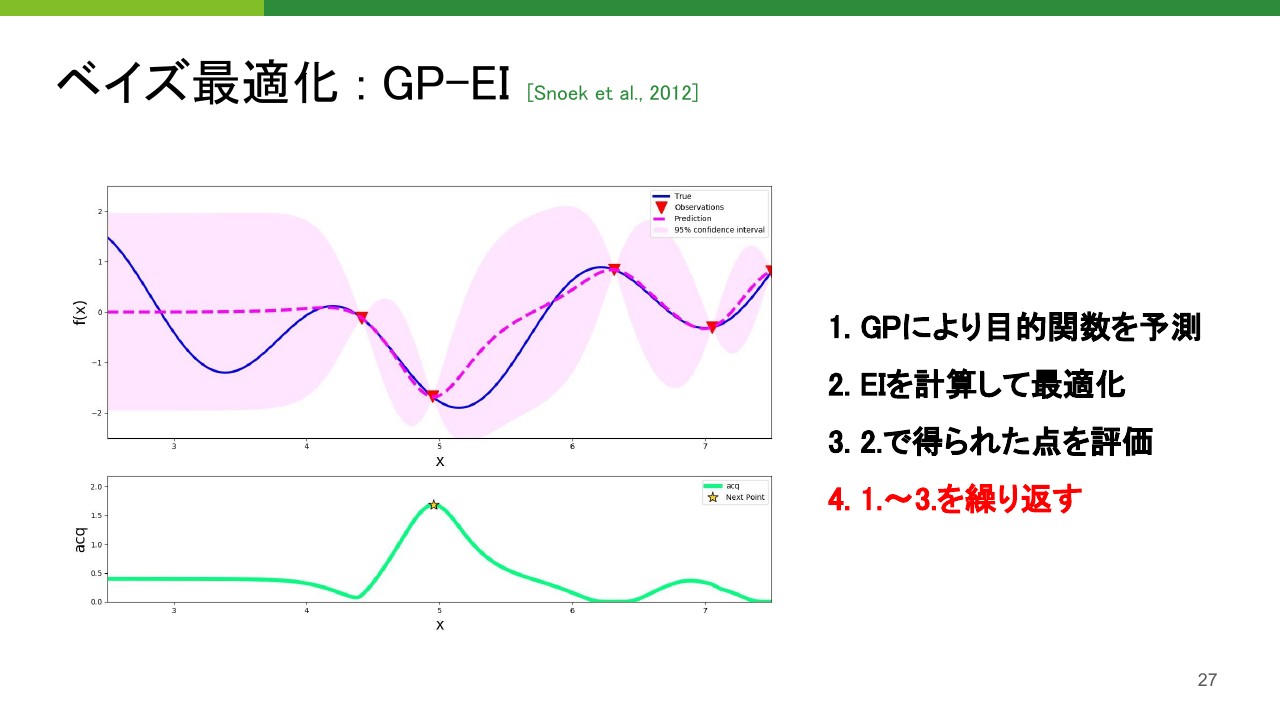
GP(ガウス過程)は、機械学習において、確率的予測モデルの一種です。ガウス分布に基づいて、入力データの分布を推定し、予測結果を計算します。GPは、RegressionやClassificiationなどのタスクに対応することができます。
GPの特徴
GPの特徴として、以下のような点が挙げられます。
- 非線形問題に強い:GPは、非線形な関係にあるデータに対しても適切に予測結果を計算できます。
- 柔軟な予測 모델:GPは、lexibleな予測モデルを提供し、様々な問題に対応することができます。
- 計算コストが高い:GPの計算には、計算コストがかかるため、大规模なデータセットには不向きです。
GPの応用
GPの応用として、以下のような例が挙げられます。
- ロボット制御:GPを用いて、ロボットの挙動を予測し、制御することができます。
- 予測モデル:GPを用いて、株価や天気などの予測モデルを構築することができます。
- 画像認識:GPを用いて、画像認識のための予測モデルを構築することができます。
GPの장점と欠点
GPの장점と欠点として、以下のような点が挙げられます。
- 장점:GPは、高精度な予測結果を計算することができます。
- 欠点:GPは、計算コストがかかるため、大规模なデータセットには不向きです。
- 改善点:GPの計算コストを低減するための研究が進められています。
よくある質問
ガウス過程回帰とは何ですか。
ガウス過程回帰とは、機械学習の手法の一つで、ガウス過程という数学的概念を用いて、回帰分析を行うものです。ガウス過程回帰は、非線形関係にあるようなデータに対しても、高精度の予測結果を得ることができます。この手法は、Bayesの定理を基にしており、モデルの複雑さを自動的に調整することができます。
ガウス過程回帰の長所は何ですか。
ガウス過程回帰の長所の一つは、柔軟なモデリングが可能ということです。ガウス過程回帰では、カーネル関数を選択することで、モデルの複雑さを自由に調整することができます。また、ガウス過程回帰は、過学習を自動的に防ぐことができます。さらに、ガウス過程回帰は、分布の推定も同時に行うことができます。
ガウス過程回帰を適用するうえでの注意点は何ですか。
ガウス過程回帰を適用するうえでの注意点の一つは、データの前処理が適切に行われていないと、予測結果が不正確になるということです。また、ガウス過程回帰では、ハイパーパラメーターの調整が必要です。ハイパーパラメーターの調整を適切に行うことで、予測結果の精度を向上させることができます。
ガウス過程回帰と他の機械学習手法の違いは何ですか。
ガウス過程回帰と他の機械学習手法の主な違いは、モデルの仮定にあるということです。ガウス過程回帰では、ガウス過程という数学的概念を用いて、非線形関係にあるようなデータを 모델化しています。一方、他の機械学習手法では、線形関係にあるようなデータをモデル化しています。また、ガウス過程回帰は、Bayesの定理を基にしており、モデルの複雑さを自動的に調整することができます。
Si quieres conocer otros artículos parecidos a 難解なガウス過程回帰をわかりやすく解説! puedes visitar la categoría Puroguramingu.