
行列式の微分をわかりやすく解説!近似との関係性も
行列式という数学の概念は、多くの学生や研究者にとって馴染み深いものです。しかし、行列式の微分という微妙な話題については、ovieselyの理解を阻む壁があります。本記事では、行列式の微分の仕組みをわかりやすく解説します。また、近似との関係性についても触れ、より深く理解することを目的としています。数学の初学者から経験者まで、行列式の微分の魅力に触れるための一つの指南書として、読者達に役立つ情報を提供します。

行列式の微分をわかりやすく解説!近似との関係性も
行列式の微分は、行列式の値の変化率を求めることを指します。strong{微分}という言葉が示す通り、微小な変化を捉えることができます。行列式の微分を理解することで、数値計算や近似計算などの様々な分野での応用が期待できます。
行列式の微分の定義
行列式の微分は、行列式の各要素の微分を総合的に捉えることを指します。具体的には、行列式Aの要素a ijの微分をΔa ijとおくと、行列式Aの微分ΔAは、次のように定義されます。
| 行列式A | 要素a ij | 微分Δa ij |
|---|---|---|
| Α | a ij | Δa ij |
行列式の微分の性質
行列式の微分には、加法性、スカラー倍性、積の微分の公式など、幾つかの性質があります。これらの性質を理解することで、行列式の微分を эффектив的に計算することができます。
近似との関係性
行列式の微分は、近似計算との関係性が深いです。strong{ニュートン法}やstrong{ガウス・ニュートン法}などの近似計算法では、行列式の微分を使用して、関数の近似値を求めることができます。
応用例
行列式の微分を応用することで、様々な分野での計算が可能になります。strong{機械学習}におけるパラメーターの更新や、strong{信号処理}におけるフィルターデザインなど、実際的な問題解決に役立つ応用があります。
計算のTips
行列式の微分の計算には、数値計算ソフトウェアやプログラミングスキルが必要です。strong{NumPy}やstrong{SciPy}などのPythonライブラリを使用することで、効率的に計算することができます。
数学で近似とは何ですか?

数学で近似とは、何ですか?
近似とは、数学的に正確な値ではなく、近い値を求めることを指します。那において、計算や測定の誤差を考慮し、実際に求めることができない値に対して、できる限り近い値を推測することを目指します。
近似の必要性
計算や測定の誤差が不可避であるため、数学的な問題には必ず近似が必要です。特に、無限小の概念が絡む問題や、超越数を含む問題では、近似が唯一の方法です。また、実際の問題では、計算や測定の誤差を無視することができないため、近似が必要不可欠です。
- 誤差の存在
- 無限小の概念
- 超越数の存在
近似の方法
近似の方法として、線形近似、多項式近似、ニュートン法などがあります。これらの方法を用いることで、数学的な問題に対して近似値を求めることができます。また、モンテカルロ法や乱数近似など、ランダムな要素を含む方法もあります。
- 線形近似
- 多項式近似
- ニュートン法
近似の限界
近似には限界があります。那において、誤差の蓄積や、計算の複雑さなどが挙げられます。また、近似の結果が誤りにおちる場合もあります。そのため、近似の結果を十分に検討し、誤りがないかを確認することが重要です。
- 誤差の蓄積
- 計算の複雑さ
- 誤りの可能性
グラフを微分すると何がわかるのか?
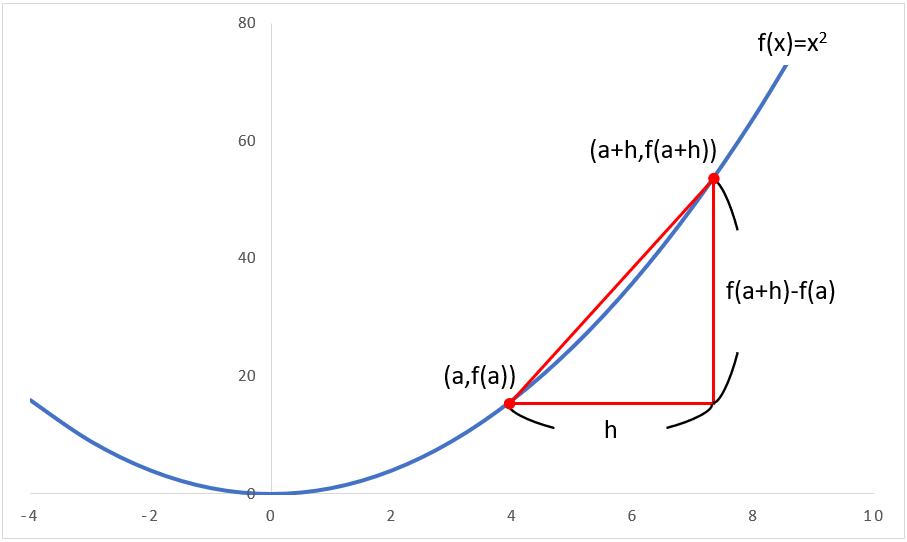
グラフを微分することで、関数の性質や挙動をより深く理解することができます。特に、グラフの傾きや曲率を微分することで、関数の最適化や安定性の分析を行うことができます。
微分の目的
微分の目的は、関数の性質や挙動をより深く理解することです。具体的には、以下のようなことがわかります。
- 関数の傾き:グラフの傾きを微分することで、関数の増加率や減少率を知ることができます。
- 関数の極値:グラフの極値を微分することで、関数の最大値や最小値を知ることができます。
- 関数の安定性:グラフの安定性を微分することで、関数の安定性や不安定性を知ることができます。
微分の方法
微分の方法として、以下のような方法があります。
- 限界値:関数の限界値を微分することで、関数の傾きや曲率を知ることができます。
- 微分係数:関数の微分係数を微分することで、関数の増加率や減少率を知ることができます。
- ニュートン法:ニュートン法を用いて、関数の極値を微分することができます。
微分の応用
微分の応用として、以下のような分野があります。
- 機械学習:機械学習において、微分を用いて、最適化問題を解くことができます。
- 制御理論:制御理論において、微分を用いて、システムの安定性を分析することができます。
- 経済学:経済学において、微分を用いて、経済指標の変化を分析することができます。
多項式近似式とは何ですか?
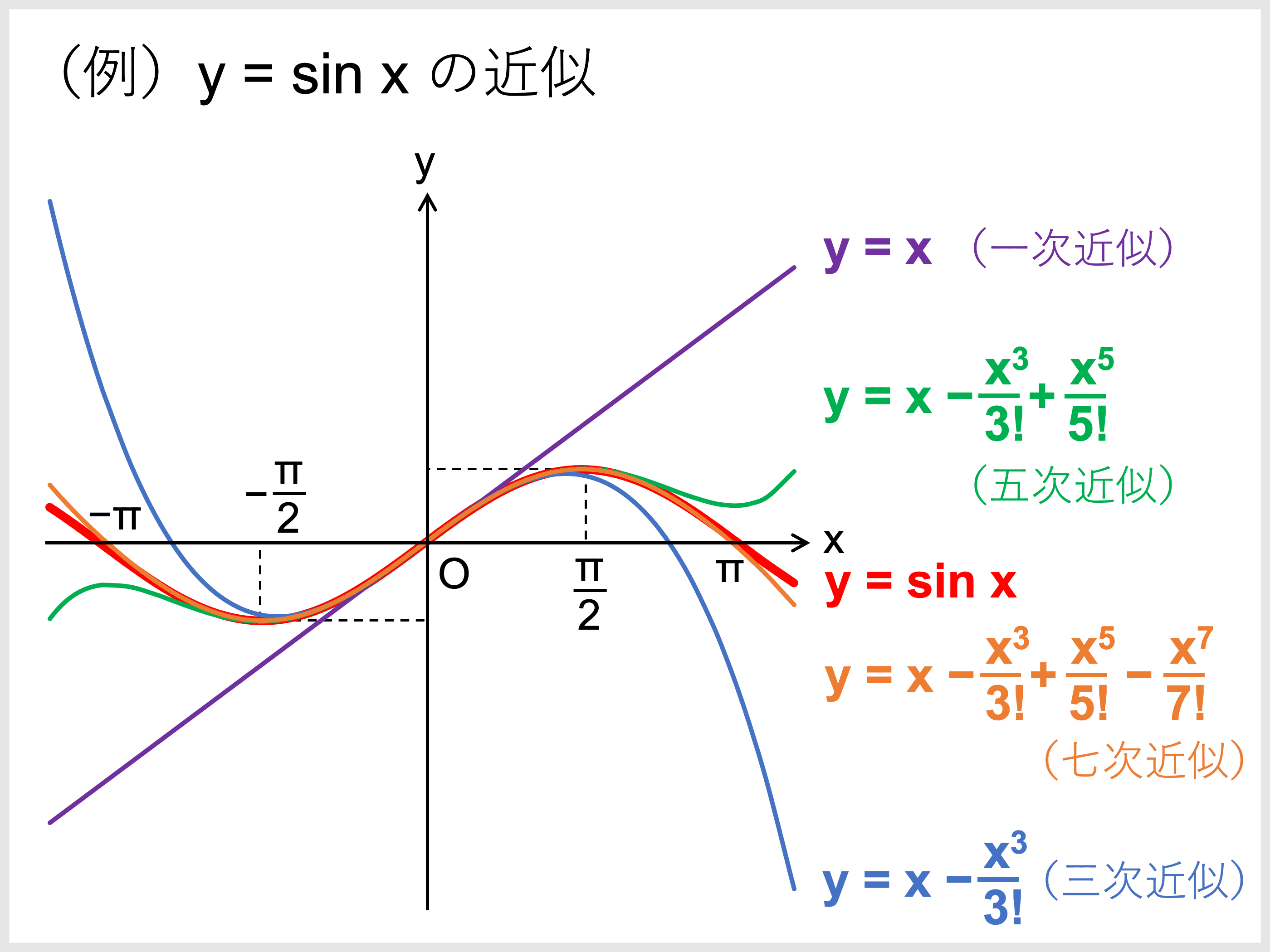
多項式近似式とは、数学における近似的手法の一種で、一つの関数をより簡単な多項式で近似することを指します。近似式の目的は、計算の簡略化や、解析の容易化にあることが多いため、多項式近似式は科学技術の分野で広く用いられています。
多項式近似式の種類
多項式近似式には、テイラー近似、マーリン近似、チェビシェフ近似など、多くの種類があります。これらの近似式は、それぞれ異なる特徴を持ち、異なる問題に対応しています。
- テイラー近似は、関数の近傍での挙動を捉えるために用いられます。
- マーリン近似は、関数の中心での挙動を捉えるために用いられます。
- チェビシェフ近似は、関数の最大値や最小値を捉えるために用いられます。
多項式近似式の利点
多項式近似式の利点として、計算の簡略化や、解析の容易化などが挙げられます。また、多項式近似式を用いることで、計算の高速化や、ミスの減少など、様々なメリットが期待できます。
- 計算の簡略化:多項式近似式を用いることで、計算の手順を簡略化できます。
- 解析の容易化:多項式近似式を用いることで、解析が容易になるため、問題の理解が深まります。
- 高速化:多項式近似式を用いることで、計算の高速化が期待できます。
多項式近似式の適用分野
多項式近似式は、科学技術の分野で広く用いられています。物理学、工学、情報科学など、様々な分野で多項式近似式が適用されています。
- 物理学:多項式近似式を用いることで、物理現象のモデル化や、シミュレーションが可能になります。
- 工学:多項式近似式を用いることで、システムの最適化や、設計が容易になります。
- 情報科学:多項式近似式を用いることで、データの解析や、予測が可能になります。
微分係数と導関数の違いは何ですか?

微分係数と導関数は、数学の分野において、関数の挙動を調べるために用いられる重要な概念です。微分係数は、関数の微小な変化に対する応答を測る mainScreening 係数であり、導関数は、関数の近傍での傾きを表す係数です。両者は、数学的には異なるが、関数の挙動を理解する上で重要な役割を果たしています。
微分係数の特徴
微分係数は、関数の微小な変化に対する応答を測る係数です。微小な変化に対する関数の応答を測ることで、関数の挙動を理解することができます。微分係数は、
- 関数の傾きを測る
- 関数の最大値・最小値を探す
- 関数の凹凸を調べる
などの用途があります。
導関数の特徴
導関数は、関数の近傍での傾きを表す係数です。傾きを表すことで、関数の挙動を理解することができます。導関数は、
- 関数の増加率を測る
- 関数の最大値・最小値を探す
- 関数の凹凸を調べる
などの用途があります。
微分係数と導関数の関係
微分係数と導関数は、数学的には異なるが、関数の挙動を理解する上で重要な役割を果たしています。両者は、関数の微小な変化に対する応答を測るために用いられます。微分係数は、導関数の_Helper_として機能し、導関数は、微分係数の_Generalization_として機能します。
- 微分係数は、導関数の特殊な場合
- 導関数は、微分係数の一般化
- 両者は、数学的には異なるが、関数の挙動を理解する上で重要な役割を果たす
よくある質問
行列式の微分とは何ですか?
行列式の微分は、行列式の値が nhỏさ変化することを研究する数学的概念です。具体的には、partial derivativeという微分の手法を用いて、行列式の各成分に関する微分係数を求めることができます。この微分係数は、行列式の値が小さ変化する場合の挙動を表現するために重要な指標です。
行列式の微分と近似の関係は何ですか?
行列式の微分と近似は、緊密な関係があります。近似とは、実際の値に近づけるための数値的近似を指します。行列式の微分を用いることで、近似の誤差を評価することができます。また、近似の誤差を小さくするために、行列式の微分係数を適切に設定することが重要です。
行列式の微分を計算する方法は何ですか?
行列式の微分を計算する方法はいくつかあります。 chain ruleという方法を用いることで、複雑な行列式の微分を簡単に計算することができます。また、product ruleという方法を用いることで、行列式の微分係数を計算することができます。さらに、numerical differentiationという方法を用いることで、数値的に行列式の微分係数を計算することができます。
行列式の微分の実際的応用例は何ですか?
行列式の微分の実際的応用例はいくつかあります。例えば、機械学習や統計学などの分野で、行列式の微分を用いて最適化問題を解くことができます。また、物理工学や制御工学などの分野で、行列式の微分を用いてシステム同定や制御系の設計を行うことができます。さらに、経済学や金融工学などの分野で、行列式の微分を用いて為替相場や株価分析を行うことができます。
Si quieres conocer otros artículos parecidos a 行列式の微分をわかりやすく解説!近似との関係性も puedes visitar la categoría Detakaiseki.






