今度こそ理解する！対数関数(log関数)の基礎

数学の世界において、対数関数は非常に重要な概念の一つです。amiliaあるいは、自然対数の名称でも知られるこの関数は、数学や科学の分野において幅広く利用されています。しかし、対数関数の基礎的な理解が足りないまま、難しい問題に立ち向かう羽目になりやすいようです。今回は、対数関数の基礎を整然と理解することを目指し、明晰な説明を通じて、数学の基礎をより深く理解することを目指します。

今度こそ理解する！対数関数(log関数)の基礎

対数関数は、数学の基礎的な概念の一つです。それは、指数関数の逆関数として定義され、様々な分野で広く用いられます。本稿では、対数関数の基礎的な概念を理解するために必要な知識を解説します。

対数関数の定義

対数関数は、指数関数の逆関数として定義されます。具体的には、指数関数の式「あ」に対する対数関数は、「loga」と記されます。対数関数は、指数関数と同じく、基数「a」と対数「x」を持つ二変数関数です。

指数関数	対数関数
a^x	loga(x)

対数関数の性質

対数関数には、以下のような性質があります。指数関数との関係も含め、様々な性質を有しています。 loga(xy) = loga(x) + loga(y) loga(x/y) = loga(x) - loga(y) loga(x^n) = nloga(x)

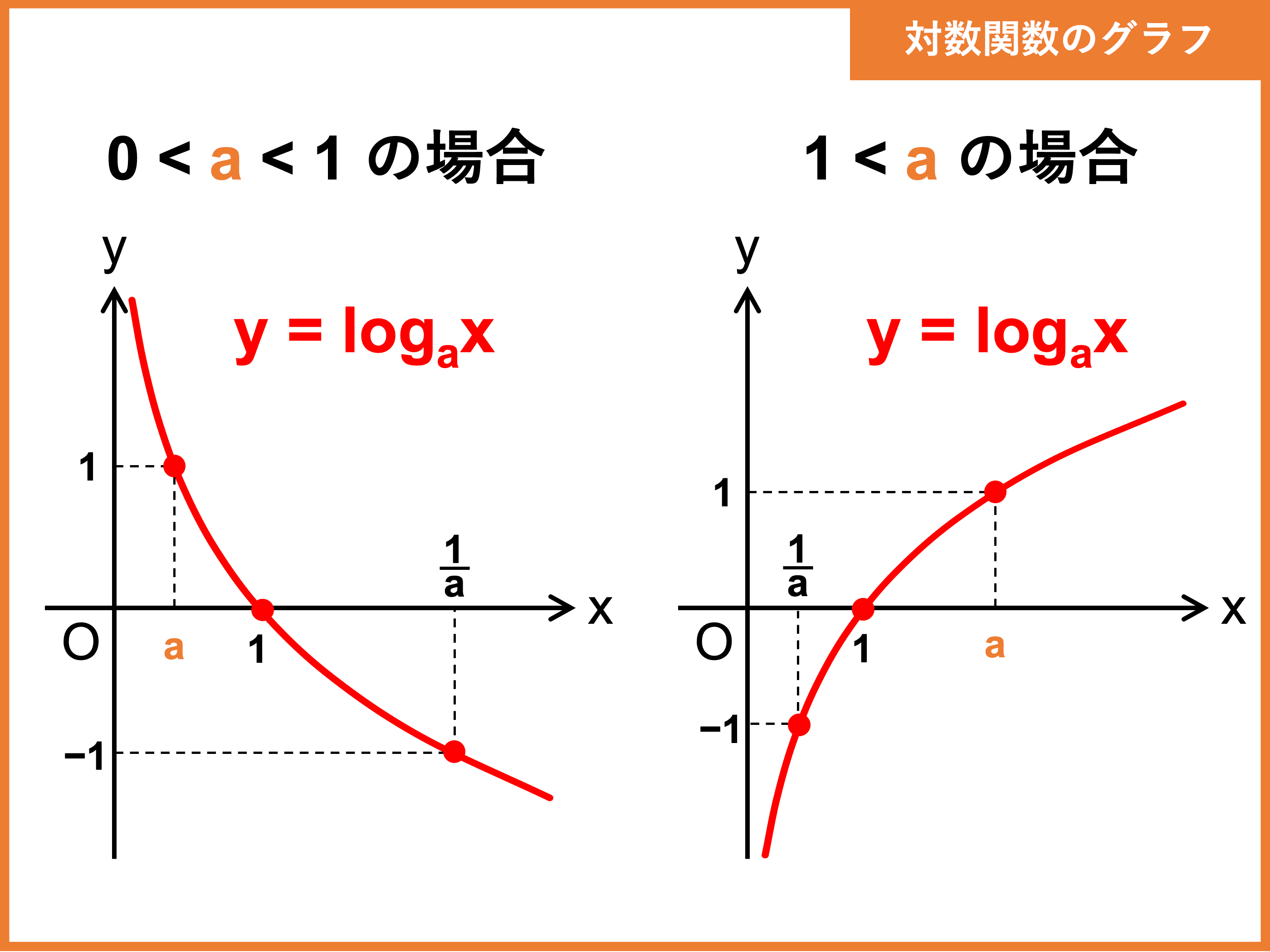
対数関数のグラフ

対数関数のグラフは、指数関数のグラフとは異なります。対数関数のグラフは、増加の速さが遅く、一定の範囲内で値が大きく変化します。

対数関数の応用

対数関数は、様々な分野で応用されます。情報理論、生物学、経済学など、広く用いられます。

対数関数の計算

対数関数の計算には、様々な方法があります。自然対数、常用対数など、基数の選択によって計算の方法が異なります。

Logは何関数ですか？

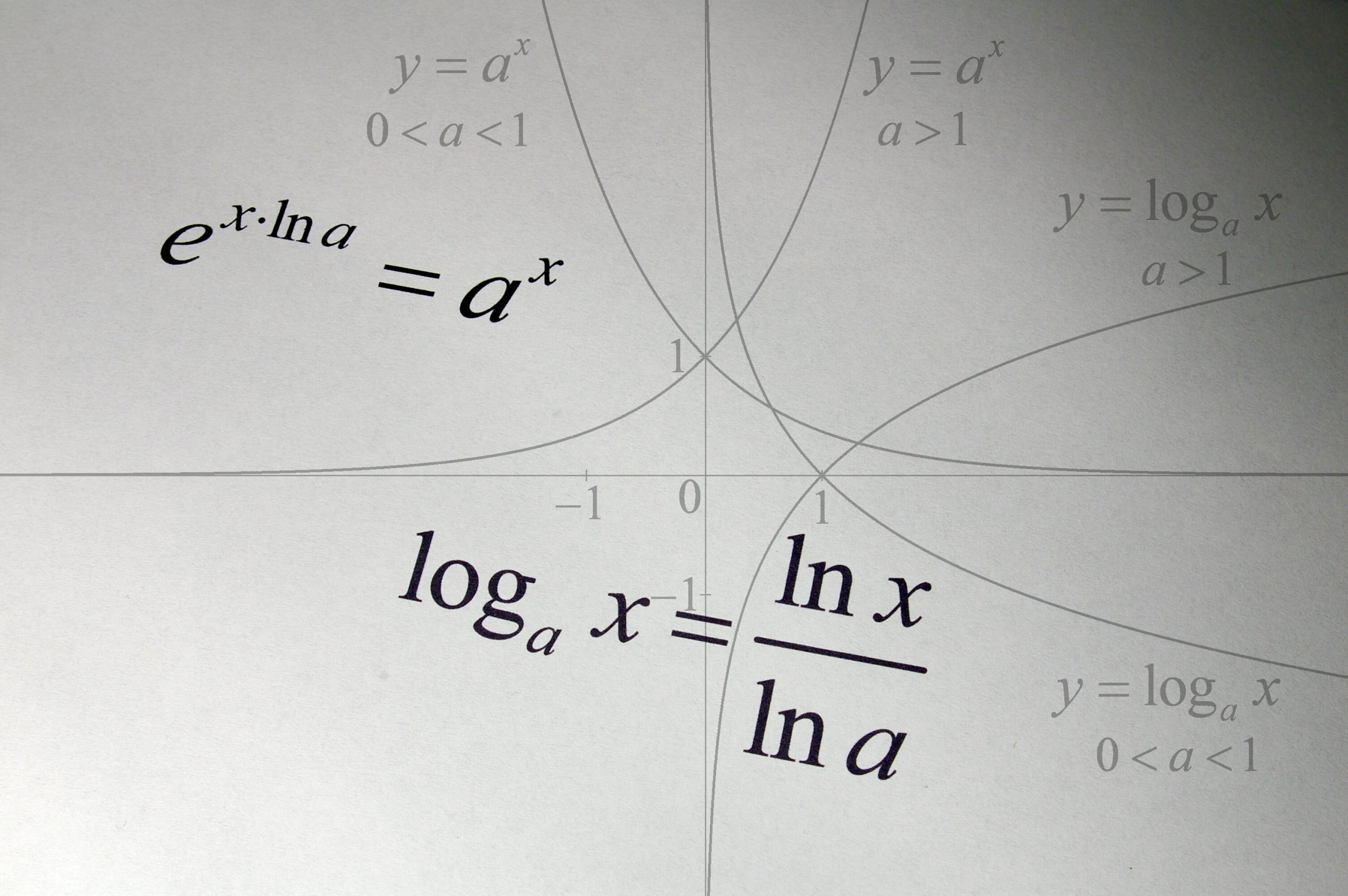
Log関数は、数学の指数関数の逆関数であり、対数関数とも呼ばれます。Log関数は、指数関数の逆操作を行い、指数関数の値を元に戻すことができます。

Log関数の性質

Log関数は、以下の性質を持っています。

対称性：Log関数は、対称性を持っており、Log(a^b) = bLog(a) という関係式が成り立ちます。
滑らかさ：Log関数は、滑らかであり、連続的に変化します。
単調増加：Log関数は、単調増加であり、入力値が大きくなるにつれて値が大きくなります。

Log関数の応用

Log関数は、さまざまな分野で応用されています。

科学計算：Log関数は、科学計算において、指数関数の逆操作を行うために使用されます。
情報理論：Log関数は、情報理論において、情報量の計算に使用されます。
経済学：Log関数は、経済学において、インフレーションの計算や資産の評価に使用されます。

Log関数の種類

Log関数には、以下のような種類があります。

自然対数：ln関数は、自然対数を計算するためのLog関数です。
common logarithm：log関数は、common logarithmを計算するためのLog関数です。
二進対数：log2関数は、二進対数を計算するためのLog関数です。

Logの底の条件は？

Logの底の条件は、システムの運用上不可欠な要件です。

ログの基本要件

ログの底の条件には、信頼性、性能、セキュリティの3つの要件が含まれます。これらの要件を満たすことで、システムの運用上の問題を回避し、 hiệu suấtの向上を実現することができます。

ログの信頼性：ログが正確に記録され、 false 情報が含まれないことを保証する。
ログの性能：ログの記録速度や容量があり、システムの性能に支障をきたさない。
ログのセキュリティ：ログに含まれる機密情報を保護し、不正アクセスから守る。

ログの詳細条件

ログの底の条件には、ログの種類、ログの形式、ログの保存期間の3つの要件が含まれます。これらの要件を満たすことで、ログの有効性を高めることができます。

ログの種類：システムの運用上必要なログの種類を指定し、不要なログを排除する。
ログの形式：ログの形式を標準化し、ログの分析や検索を容易にする。
ログの保存期間：ログの保存期間を設定し、古いログを削除する。

ログの実装方法

ログの底の条件を満たすためには、ログの記録方法、ログの分析方法、ログの監視方法の3つの方法が含まれます。これらの方法を実装することで、ログの有効性を高めることができます。

ログの記録方法：ログを正確に記録するための方法を実装する。
ログの分析方法：ログを分析し、システムの問題を把握するための方法を実装する。
ログの監視方法：ログを監視し、システムの問題を早期に発見するための方法を実装する。

対数logとはどういう意味ですか？

対数logとは、ある値のべき乗を逆転させた値を取得する数学的な操作です。対数という用語は、ギリシャ語の「logos」（言葉、理論）に由来し、17世紀のスコットランドの数学者ジョン・ナピアが導入しました。

対数logの種類

対数logには、以下のような種類があります。

自然対数（ln）：自然数eを底とする対数logです。
常用対数（log）：10を底とする対数logです。
二進対数（lb）：2を底とする対数logです。

対数logの性質

対数logには、以下のような性質があります。

対数の積の法則：対数logの積は、対数logの和に等しいという法則です。
対数の商の法則：対数logの商は、対数logの差に等しいという法則です。
指数関数との関係：対数logは、指数関数の逆関数という関係があります。

対数logの応用

対数logには、以下のような応用があります。

科学計算：対数logは、非常に大きな値や非常に小きな値を扱う科学計算において役立つ数学的操作です。
情報理論：対数logは、情報理論において、情報の数量を測るための尺度として用いられます。
経済分析：対数logは、経済分析において、経済指標の変化を測るための数学的操作です。

Log 高校何年？

ログ高校何年？

大学入試におけるログの高校年の問題について説明します。ログ高校何年という問題は、高校生が大学入試に出願する際に、高校での学年の何年目かを尋ねる問題です。この問題は、大学の入試ramesに基づいて、高校での学年の長さを尋ねることを目的としています。

ログ高校何年の問題の目的

ログ高校何年の問題は、大学入試における出願者の資格や適性を判断するために設けられています。大学入試に際しては、高校での学年の長さが考慮されます。この問題によって、出願者の高中年の実績や大学での適性を判断することができます。

ログ高校何年の問題の対策

ログ高校何年の問題に対する対策として、高校での学習経験や大学入試対策の経験を重視することが重要です。また、高校での成績や課外活動も考慮されます。出願者は、これらの経験に基づいて、大学入試での自己アピールを考える必要があります。

ログ高校何年の問題の例

以下は、ログ高校何年の問題の例です。

「高校1年生の時、どのような学習をしていたか」を尋ねる問題。
「高校2年生の時、どのような課外活動に参加していたか」を尋ねる問題。
「高校3年生の時、どのような進路を希望していたか」を尋ねる問題。

よくある質問

対数関数とは何か？

対数関数は、指数関数の逆関数であり、数値の大きさを示す尺度を変換するために使用される数学的関数です。対数関数は、自然対数や常用対数のように様々な種類があり、異なる底を使用して計算を行います。対数関数は、数学や統計学、工学など多くの分野で広く利用されており、データの分析や予測に不可欠な役割を果たしています。

対数関数の性質是什么？

対数関数には、積の対数は.sumや商の対数は差などの重要な性質があります。これらの性質を理解することで、対数関数を効率的に使用できるようになります。また、対数関数は連続性や微分可能性などの性質もあり、微積分学における重要な概念です。

対数関数はどこで使用されるの？

対数関数は、数学や統計学、工学など多くの分野で広く利用されています。例えば、確率論や統計学では、対数関数を使用してデータの分布を分析しています。また、経済学では、対数関数を使用して経済指標を分析し、将来の予測を行っています。また、工学では、対数関数を使用して信号処理や機械学習を行っています。

対数関数の計算は難しいの？

対数関数の計算は、数学的公式や計算機を使用することで容易に行うことができます。例えば、自然対数の計算には、指数関数を使用することができます。また、計算機を使用することで、対数関数の計算を高速かつ正確に行うことができます。ただし、対数関数の計算には、小数点以下の計算や換算などの注意点があります。

Si quieres conocer otros artículos parecidos a 今度こそ理解する！対数関数(log関数)の基礎 puedes visitar la categoría Puroguramingu.