2次曲線の式から楕円パラメータを導出する方法

۲次曲線の式からは、楕円のパラメータを導出することができます。楕円のパラメータとは、楕円の形を決めるための重要な値です。これらの値を正確に導出することで、楕円の形状や大きさを正しく把握することができます。この方法は、工業デザインやCADでの楕円の描画など、実際の問題に応用することができます。この記事では、２次曲線の式から楕円パラメータを導出する方法を紹介します。

2次曲線の式から楕円パラメータを導出する方法

2次曲線の式から楕円パラメータを導出する方法は、数学的に厳密な方法論をもつため、楕円曲線のパラメータを正確に導出することができます。この方法は、楕円曲線の応用分野において非常に重要です。

楕円曲線の式の種類

楕円曲線の式には、一般式、標準式、 Parameters 式などがあります。一般式は、Ax^2 + By^2 + Cxy + Dx + Ey + F = 0という形で表され、標準式は、x^2/a^2 + y^2/b^2 = 1という形で表されます。Parameters 式は、x = acos(t) - bsin(t)、y = asin(t) + bcos(t)という形で表されます。

楕円パラメータの導出の工程

楕円パラメータの導出は、以下の工程を踏みます。式の変形、パラメータの計算、結果の検証です。式の変形では、楕円曲線の式を標準式に変形します。パラメータの計算では、標準式から楕円パラメータを計算します。結果の検証では、計算結果を検証します。

式の変形の方法

式の変形には、完全平方公式や部分分数分解などの方法があります。完全平方公式は、x^2 + y^2 + 2xy + x + y = 0という形の式を、(x + y)^2 + x + y = 0という形に変形します。部分分数分解は、分母が多項式の式を、分母が単項式の式に分解します。

パラメータの計算の方法

パラメータの計算には、三角関数や複素数などの方法があります。三角関数は、三角関数の公式を使用してパラメータを計算します。複素数は、複素平面上での計算を使用してパラメータを計算します。

楕円曲線の応用分野

楕円曲線の応用分野は、電気工学、機械工学、建築学など多岐にわたります。電気工学では、フィルターや Oscillator の設計に使用されます。機械工学では、-linkage 運動の分析に使用されます。建築学では、建築物の設計に使用されます。

式の種類	楕円パラメータ	応用分野
一般式	a, b, c	電気工学
標準式	a, b	機械工学
Parameters 式	a, b, t	建築学

2次曲線の方程式は？

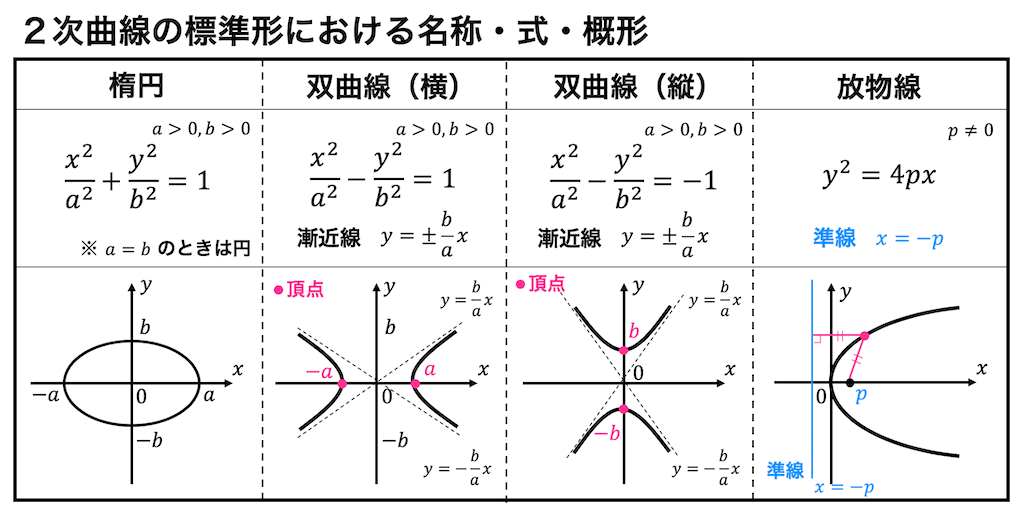
2次曲線の方程式は、$y=ax^2+bx+c$の形で表される。これは、2次関数のグラフが描く曲線の形を決定するための式である。2次曲線においては、頂点、 vertex 、:focusという重要な概念が登場する。

2次曲線の方程式の形

2次曲線の方程式は、通常、$y=ax^2+bx+c$の形で表される。この式では、$a$、$b$、$c$は定数である。aが正の値である場合、曲線は上方に開き、aが負の値である場合、曲線は下方に開く。

2次曲線の性質

2次曲線には、以下のような性質がある。

頂点を通り、軸に対して対称である。
曲線の開き方を決定するのは、aの符号である。
曲線の最小値や最大値は、頂点にあり、y座標はそこで最小値や最大値になる。

2次曲線の応用

2次曲線は、様々な分野で応用される。

物理学での運動の軌跡の描き方
経済学での需要曲線や供給曲線の描き方
工学での構造物の形状の設計

楕円になる条件は？

楕円になる条件は、平面上に存在する3点が一直線上にないことです。すなわち、3点が同一直線上にない場合、その3点を通る曲線が楕円になる可能性があります。

楕円の定義

楕円は、原点を中心として、焦点をもつ二次曲線です。焦点は、楕円の形を決める要素であり、楕円の中心から等距離にある2つの点を結ぶ線分の長さに応じて、楕円の形が変化します。

楕円の条件

楕円になる条件は、以下の3点を満たすことです。

3点が一直線上にないこと
3点を通る曲線が閉じていること
曲線が連続的に変化すること

これらの条件を満たす場合、3点を通る曲線が楕円になる可能性があります。

楕円の性質

楕円には、以下のような性質があります。

対称性：楕円は、中心に対して対称です。
連続性：楕円は、連続的に変化します。
閉じている：楕円は、閉じている曲線です。

これらの性質を考慮することで、楕円の形状をより良く把握することができます。

楕円を表す方程式は？

楕円を表す方程式は、 $(x-h)^2/a^2 + (y-k)^2/b^2 = 1$ である。これは、楕円の中心が $(h, k)$、長半径が $a$、短半径が $b$ である場合の標準形の方程式である。

楕円の方程式の導出

楕円の方程式は、幾何学的には、楕円の定義から導出することができる。焦点距離の公式を利用して、楕円の中心を通過する直線上の点と、楕円の焦点との距離を計算し、等式にまとめることで楕円の方程式を得ることができる。また、座標変換を施すことで、楕円の方程式を簡単に導出することもできる。

楕円の方程式の性質

楕円の方程式には、幾何学的な性質が多く含まれている。対称性という性質があり、楕円の中心を通る軸に対して対称である。また、周期性という性質があり、楕円上の点を中心として、特定の距離ごとに周期的に配置される。

楕円の方程式の応用

楕円の方程式は、実際の問題に対して多くの応用があり、天文学や物理学、機械工学などの分野で広く用いられている。また、楕円の方程式を基礎にして、より高度な数学的な理論を構築することもできる。

楕円の面積や周囲長を計算する。
楕円上の点の座標を計算する。
楕円と他の幾何学図形との交点を計算する。

楕円とはどのような曲線ですか？

楕円とは、楕円形の曲線を指します。楕円は、中心点を含む長軸と短軸の2つの軸を持つ閉じた曲線です。この曲線を描くには、中心点から等距離にある2つの点を通るように長軸と短軸を描き、両軸を交わる点を中心点として曲線を描きます。

楕円の性質

楕円は、以下の性質を持っています。

閉じた曲線：楕円は、始点と終点が同じ点にある閉じた曲線です。
対称性：楕円は、中心点に対して対称です。
軸の長さ：楕円には、長軸と短軸があり、それぞれの長さが異なります。

楕円の種類

楕円には、以下のような種類があります。

正楕円：長軸と短軸が等しい長さを持つ楕円です。
偏楕円：長軸と短軸が異なる長さを持つ楕円です。
退化楕円：長軸がなく短軸しかない楕円です。

楕円の応用

楕円は、以下のような分野で応用されます。

天文学：楕円軌道を描く惑星や衛星の軌道を研究するために使用されます。
工学：楕円形の機械部品の設計や製造に使用されます。
美術：楕円形の絵具や装飾デザインに使用されます。

よくある質問

2次曲線の式から楕円パラメータを導出する方法はあるの?

楕円パラメータを導出する方法はいくつかあります。二次曲線の式を用いることで、楕円の中心座標、半径、傾きなどを計算することができます。具体的には、式の係数を用いて楕円の標準形に変換し、パラメータを導出することができます。また、回転楕円の場合には、回転行列を用いて式を変換し、パラメータを導出することができます。

楕円の中心座標を計算するための式は?

楕円の中心座標を計算するための式は、二次曲線の式の係数を用いて計算することができます。中心座標の計算式は、一般的に次のようになります。x座標は、-b / 2a、それにy座標は、-c / 2bです。これらの式を用いることで、楕円の中心座標を計算することができます。

楕円の半径を計算するための式は?

楕円の半径を計算するための式は、二次曲線の式の係数を用いて計算することができます。半径の計算式は、一般的に次のようになります。長半径は、√(a^2 - b^2) / a、それに短半径は、√(b^2 - c^2) / bです。これらの式を用いることで、楕円の半径を計算することができます。

楕円パラメータの導出に必要な条件は?

楕円パラメータの導出には、二次曲線の式の係数が必要です。係数の条件として、a > 0、b > 0、c > 0という条件が必要です。また、楕円の標準形に変換するには、式の係数を用いて強制的に楕円の中心座標を原点に移動する必要があります。これらの条件を満たすことで、楕円パラメータを正確に導出することができます。

Si quieres conocer otros artículos parecidos a 2次曲線の式から楕円パラメータを導出する方法 puedes visitar la categoría Puroguramingu.