
A/Bテスト結果をカイ二乗検定で検証!
A/Bテストは、マーケティングやプロダクト開発において、決断的な判断材料を得るための有効なツールです。ただし、A/Bテストの結果を単に信頼するわけにはいかず、統計的手法による検証が必要です。特に、カイ二乗検定は、A/Bテストの結果を検証する上で非常に有効です。この検定は、サンプル_SIZEや検出力に影響されないため、より正確な結果を得ることができます。本稿では、A/Bテストの結果をカイ二乗検定で検証する方法を紹介します。

A/Bテスト結果をカイ二乗検定で検証!
A/Bテスト結果をカイ二乗検定で検証することで、より効果的なマーケティング戦略を立てることができます。カイ二乗検定は、統計学的手法の一種で、二つのグループ間に有意な差があるかどうかを検証するために使用されます。A/Bテスト結果をカイ二乗検定で検証することで、テスト結果の信頼性を高めることができます。
カイ二乗検定の原理
カイ二乗検定は、統計学的手法の一種で、二つのグループ間に有意な差があるかどうかを検証するために使用されます。仮説と呼ばれる予想の真偽を検証するために、標本データを分析します。カイ二乗検定では、自由度、検出力、有意水準などを設定し、検証結果を計算します。
A/Bテスト結果の検証
A/Bテスト結果をカイ二乗検定で検証することで、テスト結果の信頼性を高めることができます。標本データを分析し、対象グループ間に有意な差があるかどうかを検証します。テスト結果が有意的である場合、対象グループ間に実際にある差があると考えられます。
検証結果の解釈
検証結果を解釈することで、A/Bテスト結果の信頼性を高めることができます。p値が有意水準以下である場合、対象グループ間に実際にある差があると考えられます。そうでない場合、対象グループ間に実際にある差はないと考えられます。
検証の例
以下は、A/Bテスト結果をカイ二乗検定で検証する例です。
| 対象グループ | Aグループ | Bグループ |
|---|---|---|
| 購入率 | 20% | 30% |
| クリック率 | 15% | 20% |
検証の注意点
A/Bテスト結果をカイ二乗検定で検証する際には、注意する点がいくつかあります。標本データの質や、検証の設定ミスなどを避ける必要があります。また、検証結果を誤解釈しないように注意する必要があります。
カイの二乗検定で何がわかるのか?

カイの二乗検定は、統計学における仮説検定の一種で、観測データに込められた二乗の関係を検定するために用いる。
検定の目的
カイの二乗検定の目的は、観測データが 独立した分布に従うかどうかを検定することである。独立という言葉どおり、各データが互いに独立しており、どのデータも他のデータに影響を受けていないかどうかを調べる。
検定の手順
カイの二乗検定の手順は、以下の通りである。
- 仮説の設定:観測データが独立した分布に従うという仮説を設定する。
- 検定統計量の算出:観測データに基づいて検定統計量を算出する。
- p値の算出:検定統計量に基づいてp値を算出する。
- 仮説の棄却:p値が有意水準以下の場合、仮説を棄却する。
検定結果の解釈
カイの二乗検定の結果は、p値によって解釈する。p値が有意水準以下の場合、観測データは独立した分布に従わず、相関があると考えられる。一方、p値が有意水準以上の場合、観測データは独立した分布に従うと考えられる。
効果検証のABテストとは?
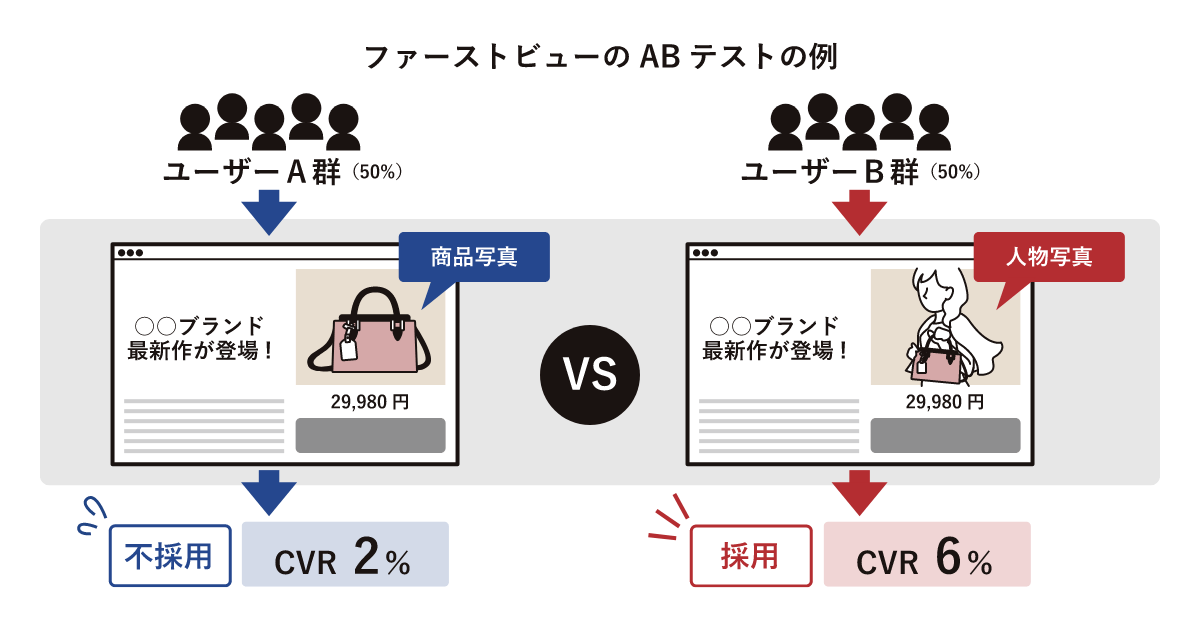
効果検証のABテストとは、ウェブサイトやアプリケーションにおいて、2つの異なるバージョン(AとB)を比較し、どちらのバージョンがより効果的であるかを検証することを指します。这により、効果的なデザインやマーケティング戦略を実現することができます。
ABテストの目的
ABテストの目的は、ウェブサイトやアプリケーションのパフォーマンスを改善し、ユーザーのエンゲージメントやコンバージョン率を向上させることです。具体的には、以下の目的があります。
- ウェブサイトやアプリケーションのデザインやレイアウトの最適化
- マーケティング戦略の効果的な実施
- ユーザーの行動や嗜好の分析
ABテストのタイプ
ABテストには、2つの主要なタイプがあります。
- スプリットテスト:ウェブサイトやアプリケーションの2つの異なるバージョンを比較する
- Multivariateテスト:複数の要素を同時にテストする
ABテストの利点
ABテストには、以下のような優位性があります。
- データに基づいた決断ができる
- 費用対効果が高まる
- ユーザーのニーズに応じたデザインやマーケティング戦略を実現できる
Z検定とカイ二乗検定の違いは何ですか?

検定の目的
Z検定とカイ二乗検定は、異なる検定の目的を持っています。Z検定は、母集団の平均値が既知の場合に、標本の平均値が母集団の平均値と異なるかどうかを検定するために用いられます。一方、カイ二乗検定は、標本の分布が母集団の分布と異なるかどうかを検定するために用いられます。
検定の目的の例:
- Z検定:医薬品の平均効果が既知の値より高い(or低い)かどうかを検定する。
- カイ二乗検定:世代別の性別比率が母集団の性別比率と異なるかどうかを検定する。
検定の仮説
Z検定とカイ二乗検定では、検定の仮説が異なります。Z検定では、零仮説が「標本の平均値は母集団の平均値と等しい」というものであり、対立仮説が「標本の平均値は母集団の平均値と異なる」というものです。一方、カイ二乗検定では、零仮説が「標本の分布は母集団の分布と等しい」というものであり、対立仮説が「標本の分布は母集団の分布と異なる」というものです。
検定の仮説の例:
- Z検定:零仮説「平均血圧は120mmHg」、対立仮説「平均血圧は120mmHg以外」。
- カイ二乗検定:零仮説「性別比率は1:1」、対立仮説「性別比率は1:1以外」。
検定の統計量
Z検定とカイ二乗検定では、検定の統計量が異なります。Z検定では、Z統計量として、標本の平均値と母集団の平均値との差を標準化した値を用います。一方、カイ二乗検定では、カイ二乗統計量として、標本の分布と母集団の分布との差を測るために用いられます。
検定の統計量の例:
- Z検定:Z=(x-μ)/σ、 where x is the sample mean, μ is the population mean, and σ is the population standard deviation。
- カイ二乗検定:χ2=Σ[(observed frequency - expected frequency)^2 / expected frequency]、 where observed frequency is the frequency of each category in the sample, and expected frequency is the frequency of each category in the population。
T検定とカイ二乗検定の違いは何ですか?

検定の目的の違い
T検定とカイ二乗検定は、目的が異なる検定方法です。T検定は、2つのグループ間の平均値の差を検定するために使用されます。一方、カイ二乗検定は、2つのGridView間の独立性を検定するために使用されます。例えば、T検定では、男女の平均身長の差を検定することができます。一方、カイ二乗検定では、性別と血液型との関係を検定することができます。
検定統計量の違い
T検定とカイ二乗検定では、検定統計量が異なります。T検定では、t統計量が用いられます。一方、カイ二乗検定では、カイ二乗統計量が用いられます。t統計量は、2つのグループ間の平均値の差を基準にして計算されます。一方、カイ二乗統計量は、観測された頻度と期待される頻度との差を基準にして計算されます。
- T検定:t統計量=( Grupo1の平均値-Grupo2の平均値 ) / ( Grupo1の標準偏差 / √n)
- カイ二乗検定:χ²統計量=Σ[(観測された頻度-期待される頻度)^2 / 期待される頻度]
適用_WHYPの違い
T検定とカイ二乗検定は、適用_WHYPが異なります。T検定は、正規分布に従う連続的なデータに対して適用されます。一方、カイ二乗検定は、離散的なデータに対して適用されます。例えば、T検定では、身長や体重のような連続的なデータを検定することができます。一方、カイ二乗検定では、性別や血液型のような離散的なデータを検定することができます。
- T検定:連続的なデータ、正規分布
- カイ二乗検定:離散的なデータ、独立性の検定
よくある質問
A/Bテスト結果をカイ二乗検定で検証する理由は何ですか?
カイ二乗検定は、A/Bテストの結果を検証するための 有効的な手法 です。この検定を行うことで、A/Bテストの結果が偶然によるものか、実際に有意差があるかどうかを 科学的に 判断することができます。特に、A/Bテストにおけるサンプルサイズが小さい場合や、結果に バイアス が存在する場合には、カイ二乗検定は有効です。
カイ二乗検定を行うための前提条件は何ですか?
カイ二乗検定を行うためには、 独立なサンプル が必要です。また、各グループの サンプルサイズ も同じである必要があります。また、A/Bテストの結果が 二項分布 に従うことも前提条件として必要です。これらの条件を満たすことで、カイ二乗検定の結果が 信頼できる ものとなるでしょう。
カイ二乗検定のp値とは何ですか?
p値は、カイ二乗検定の結果として算出される 確率値 です。このp値が 有意水準 以下である場合、A/Bテストの結果が偶然によるものではなく、実際に有意差があると 結論 づけることができます。一般的には、p値が0.05以下である場合には、有意差があると判断されます。
カイ二乗検定の結果を実際のビジネスに活用する方法は何ですか?
カイ二乗検定の結果を実際のビジネスに活用するためには、 データドリブン な意思決定を行うことが必要です。検定結果に基づいて、 最適な戦略 を選択し、 顧客体験 を向上させることができます。また、検定結果を フィードバック として、次のA/Bテストの計画に役立つ情報として活用することもできます。
Si quieres conocer otros artículos parecidos a A/Bテスト結果をカイ二乗検定で検証! puedes visitar la categoría Detakaiseki.






