基本情報技術者試験対策: 2進数で表すと無限小数になるもの
情報技術者試験は、情報処理の技能を측定するedlaの試験です。この試験で問われる問題の中には、数学的な問題も多く含まれています。특히、2進数の問題は、情報技術者にとって不可欠な知識です。この中にあって、2進数で表すと無限小数になるものについて取り上げます。このような数値を正しく理解し、計算する術を身に付けなければならない情報技術者にとって、;!vap任意の参考資料ではございません。

2進数表現での無限小数の対策
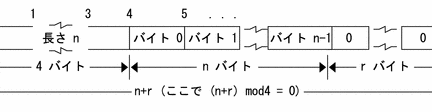
2進数表現では、10進数での有限小数が無限小数になる場合がある。これは、コンピューターの内部での数値表現の問題によるものである。基本情報技術者試験対策として、2進数表現での無限小数の問題を理解し、適切に対処する必要がある。
2進数表現の制限
コンピューター内部では、数値を2進数表現で表すことが多い。しかし、2進数表現には制限があり、10進数での有限小数を正確に表現できない場合がある。これは、2進数表現の桁数に限りがあるため、無限小数になることがある。
| 2進数表現 | 10進数表現 |
|---|---|
| 0.1 | 0.1 |
| 0.01 | 0.01 |
| 0.001 | 0.001 |
| ... | ... |
無限小数の例
10進数での有限小数が2進数表現では無限小数になる例として、0.1や0.2などの数値がある。これらの数値を2進数表現で表すと、桁数が増加するにつれて桁が繰り返し、無限小数になる。 0.1を2進数表現で表すと、0.00011001100110011...になる。
問題の対策
基本情報技術者試験対策として、2進数表現での無限小数の問題を適切に対処する必要がある。この問題に対処するため、数値の丸め処理や、桁数の増加を行うことがある。
数値の丸め処理
数値の丸め処理は、2進数表現での無限小数を問題なく扱うための方法である。丸め処理では、桁数を切り捨てて、有限小数に近似することになる。
桁数の増加
桁数の増加は、2進数表現での無限小数を問題なく扱うための方法である。桁数を増加することで、有限小数に近似することができる。
2進数で表すと無限小数になるものは?

2進数で表すと無限小数になるものは、有限小数でない十進数を2進数に変換すると無限小数になる値です。これらの値には、有限小数に対応する2進数の桁数が無限大になるため、コンピューターの浮動小数点数の計算では丸め誤差が生じます。
2進数の無限小数の例
2進数で表すと無限小数になる値の例として、以下のような十進数があります。
- 1/3 = 0.3333... (二進法では0.010101...)
- 2/3 = 0.6666... (二進法では0.101010...)
- 1/7 = 0.142857142857... (二進法では0.0010111...)
コンピューターの浮動小数点数と丸め誤差
コンピューターの浮動小数点数では、二進法で表す値に丸め誤差が生じます。この丸め誤差は、有限桁数での計算による誤差であり、計算結果に影響を与える場合があります。IEEE 754という浮動小数点数の標準では、二進法での丸め誤差を考慮した値の表現方法を定めています。
無限小数の計算と丸め誤差の対策
無限小数を計算する場合、丸め誤差の影響を最小限度に留めるため、以下のような対策をとることができます。
- 丸め誤差の訂正:計算結果に丸め誤差が生じた場合、訂正を行うことで誤差を最小限度に留める。
- 高精度計算:高精度の浮動小数点数を使用することで、丸め誤差を最小限度に留める。
- 数値計算のアルゴリズムの改良:数値計算のアルゴリズムを改良することで、丸め誤差の影響を最小限度に留める。
2進数で表せない数とは?
小数の問題
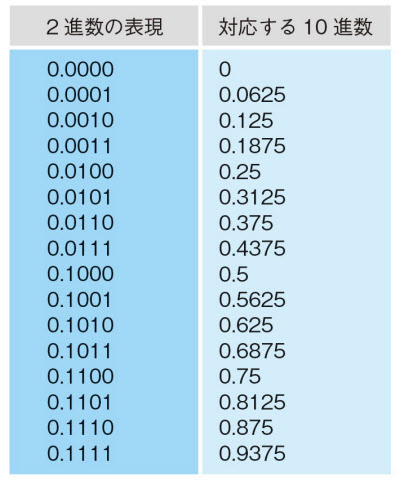
小数を2進数に変換する際、無限小数になる場合がある。その場合、有限桁で表現することができないため、2進数で表せない数となる。
- 例えば、十進数の0.1は、二進数では0.00011001100110011…と無限小数になる。
- このような場合、コンピューターでは有限桁で丸められるため、誤差が生じる。
- そのため、金融計算や科学計算のような高い精度が要求される分野では、二進数の問題点として扱われる。
根号の問題
根号は、2進数では正確に表現することができない。
- 例えば、√2は、二進数では1.0110101000001011…と無限小数になる。
- このような場合、コンピューターでは近似値を用いる必要があり、誤差が生じる。
- そのため、幾何学や物理学のような根号を頻繁に用いる分野では、二進数の問題点として扱われる。
不動小数点の問題
不動小数点は、コンピューターが小数を内部的には固定小数点数として扱う方式である。
- この方式では、小数点の位置が固定されているため、2進数での表現に制限が生じる。
- その結果、指数部と mantissa 部の両方で誤差が生じる。
- そのため、浮動小数点数方式に比べ、不動小数点方式では誤差が生じやすく、二進数の問題点として扱われる。
無限小数とは何ですか?
無限小数とは、何ですか?
無限小数は、有限小数とは異なり、少数部が無限に続く小数を指します。有限小数とは、少数部が有限の桁数しか持たない小数で、例えば、0.5や0.25などの小数を指します。一方、無限小数は、少数部が無限に続くため、有限小数とは異なる性質を示します。
無限小数の例
無限小数の例として、円周率πや自然対数eなどがあります。これらの数値は、少数部が無限に続くため、無限小数として知られています。
無限小数の特徴
- 少数部が無限に続くため、桁数が有限であることはない。
- 有限小数とは異なる性質を示す。
- 計算機上では、近似値として扱われる。
無限小数の重要性
無限小数は、数学や科学など広い分野で重要な役割を果たしています。円周率πや自然対数eなどの無限小数は、数学の基礎的概念として扱われ、広い範囲の応用を持っています。また、科学分野では、無限小数が含まれる数式が多く現れるため、無限小数の理解が重要です。
よくある質問
基本情報技術者試験対策では、2進数で表すと無限小数になるものとは何ですか。
2進数 において、無限小数になるものは、循環小数 です。循環小数とは、十進数では有限小数だが、2進数では無限小数になる数のことを指します。例えば、十進数の0.1は、2進数では0.00011001100110011…となるため、無限小数になります。
無限小数になる数値はどのような特徴がありますか。
無限小数になる数値は、分数 であることが多く、素因数 に2や5以外の数が含まれている場合、2進数では無限小数になります。また、循環節 の長さが有限の場合、十進数では有限小数だが、2進数では無限小数になる場合もあります。
基本情報技術者試験対策では、2進数の無限小数をどのように扱いますか。
基本情報技術者試験対策では、2進数の無限小数を扱う際は、近似値 や丸め を使用して扱うことが多います。また、計算機科学では、浮動小数点数 を用いて、2進数の無限小数を近似的に表現することがあります。
2進数の無限小数を扱う上では、どのような注意点がありますか。
2進数の無限小数を扱う上では、丸め誤差 や桁あふれ に注意する必要があります。また、計算結果の暗黙の精度 に留意し、計算の信頼性 を確保することが大切です。
Si quieres conocer otros artículos parecidos a 基本情報技術者試験対策: 2進数で表すと無限小数になるもの puedes visitar la categoría Puroguramingu.